化すればΦ1が変化し、Φ1の一部Φ2もまた変化し、電磁誘導によって二次コイル（S）に起電力が生じる。この現象を相互誘導という。

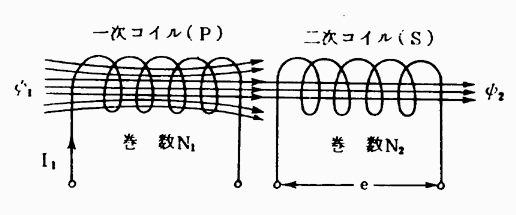
図2・20

2・8・2相互インダクタンス

上記二次コイル（S）における起電力esは次のようになる。

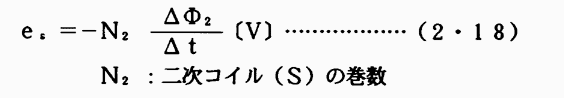
自己インダクタンスの場合の（2・17）式と同様に磁束と電流は比例するから

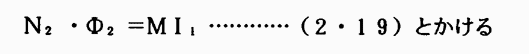
とかける

（2・19）式を（2・18）式に代入して

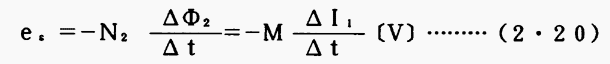
ここで、Mは相互インダクタンスと呼ばれ、二つのコイルの形状、相互位置及びその周囲の物質の透磁率によって定まる値である。相互インダクタンスも単位はLと同じくヘンリーである。

（5・20）式から

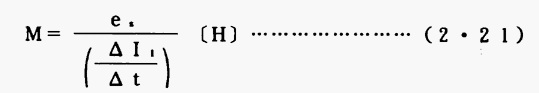
また、

と表される。

2・9 電磁結合

図2・20のようにPとSとのコイルが、磁束を仲介として結合しているとき二つのコイルPとSは電磁結合しているという。今Pコイルの自己インダクタンスをL1、Sコイルの自己インダクタンスをL2、相互インダクタンスをMとしてこれらの関係をみよう。

前ページ　　　目次へ　　　次ページ